Les nœuds :
Officiellement, il n’existe aucun nœud dans la nature : On n’y
connaît aucun nœud structurellement durable ; même les araignées ne
tissent pas de nœuds.
On dirait que la nature évite soigneusement de faire des nœuds. La
nature a horreur des nœuds. Pourquoi et comment ?
Le principe des nœuds est extrêmement simple : Plus on tire sur
deux brins et plus ça ferme ce qui est dans le nœud. Le principe de la nature
au contraire est un principe d’ouverture, et d’éternelle création.
Il est impossible de faire un nœud si on ne le pense pas fini. Mais au
contraire si on le pense fini, tout devient simple. De fait, il en va de même
pour son contraire : « pour ne pas faire de nœuds ! »
Tout dans la nature est fait pour ne pas faire de nœuds.
La nature est simple parce qu’elle pense toujours la fin - ou plutôt,
même au-delà de la fin des fins. le noeud lui serait fatal !
Tout le monde a déjà eu l’intuition que la nature joue avec le temps -
ou se joue du temps, ignore cette catégorie.
Les nœuds sont sans doute apparus avec les hommes préhistoriques et
leurs vêtements, mais ont aussi colonisé beaucoup d’industries.
Il est étrange que la géométrie des nœuds soit tellement en retard sur
toutes les autres.
Pour être plus précis, il faudrait citer les débats sur l’ADN
et l’anguille visqueuse :
1. Les très
curieuses molécules d’ADN, longues de près d’un mètre et larges de 2 nanomètres
(milliardième de mètre) pelotonnées dans la cellule et dont les 2 brins de la
double hélice se séparent lors de la reproduction cellulaire par méiose ou par
mitose sous l’effet d’enzymes. L’existence de vrais nœuds y est discutée.
2. la
surprenante anguille visqueuse qui se noue elle-même un temps limité
« en nœud trèfle » dans quelques situations
particulières :
|
|
La nodologie est l’une des plus belles inventions de l’homme, et
elle est pour beaucoup dans l’avancement de la civilisation. Historiquement,
elle prolonge peut-être l’utilisation des lianes des forêts.
Je crois que quand on aime les nœuds, on ne peut pas aimer le feu, la
fusion, la soudure, le fer, Vulcain,
les brûlures et toutes ces choses…
Avec des cordes et du bois, en mer, on peut faire presque autant de
choses qu’avec le métal, hormis l’ancre de marine. Autrefois on utilisait des
pierres.
Les meilleurs bateaux en bois sont toujours indiens, construits à
Calicut et n’ont pas un gramme de fer : Ils sont chevillés en bois pour
éviter la rouille. Le bois et les cordes, c’est la subtilité de l’esprit…
L’essentiel d’un nœud, en pratique (et c’est pourquoi
il n’en existe pas plus d’une vingtaine utiles à bien connaître ) c’est… qu’il soit facile à défaire !
Avec des leviers et des nœuds, c’est incroyable tout ce que l’on peut
faire : c’est ce qu’avait montré Archimède aux Syracusains en
relevant le défi de tirer tout seul un énorme bateau sur une plage.
|
Topologie :
Qu’est-ce qu’un nœud : Nœud ou pas nœud ? La topologie est une science née au XIXéme siècle : C’est la science du
« topos » En
grec, « topos » signifie « lieu, espace, région »
dans le sens de quelque chose d’un peu plus étendu que ce que désigne le mot
« locus » en latin. Son
étymologie est inconnue. Ce mots grec est d’une utilisation plutôt rare dans
l’Antiquité, presque plus rare qu’en français moderne où il est même devenu
fréquent (bio-tope, etc.) après avoir commencé à être vulgarisé par
l’usage qu’en fit Thomas More dans son livre « Utopia »
- mis pour « ou-topos » = « sans lieu » Le
mot utopie a fait fortune depuis. Pour
nous, depuis le début du XXème siècle, notre imagination de l’espace est
devenue intrinsèquement liée à celle du temps. Mais
tout cela est si difficile à dire – bien que les mots redondants pour dire la
vie abondent - qu’on en retient seulement en topologie l’idée de progression
ordonnée. La
science des nœuds en fait partie. Voyons
la présente manipulation, en invitant le lecteur à aller plus loin de façon
quasi-ludique grâce à la bande dessinée de J. P. Petit le « Topologicon »
.
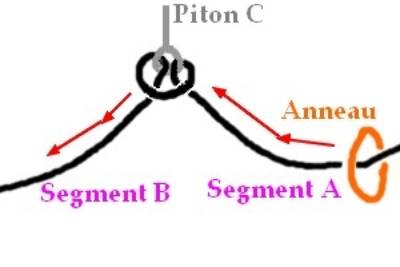
L’anneau
doit passer de A à B : Perplexité ! Pour aller
du segment A au segment B, l’anneau ne peut pas traverser le trou du piton C,
mais les cordes le peuvent. Réflexion : ·
Selon le
dessin, Il existe : un plan du piton (celui de la feuille) qui divise
tout l’espace en « espace antérieur » et « espace
postérieur » et un plan de symétrie vertical et perpendiculaire à cette
page passant par le piton (divisant chacun des espaces en deux : droit
et gauche), et l’on demande seulement à l’anneau de traverser ce second plan.
On peut donc envisager de faire 2 opérations successives inverses et
symétriques en rapprochant l’anneau du piton puis en l’éloignant. On va voir
qu’il faut diviser chacun des quarts d’espace ainsi décrits en deux par des
plans verticaux parallèles, ce qui va donner 4 espaces en avant et 4 espaces
en arrière, soit 8 portions d’espace, dont on pourra appeler les seules 4
portions proches du centre « espaces utiles », en fait champ des
opérations de passages au travers du trou du piton. ·
L’anneau ne
peut circuler que dans les deux « demi-espaces antérieurs » sans
même ne pouvoir passer de l’un à l’autre. ·
A l’inverse,
les 2 ganses occupent les deux demi-espaces latéraux à droite et à gauche, et
circulent librement entre l’avant et l’arrière ·
Ainsi chacun
des 4 quarts d’espaces est occupé, mais le trou du piton suffit à empêcher le
passage de l’anneau « des espaces avants » vers les « espaces
arrières » Or l’anneau semblerait devoir faire un aller et retour en
passant par le trou du piton pour cela. ·
Donc on va
choisir de faire toutes les opérations dans tout l’espace avant puisque le
piton n’empêche pas de faire passer toutes les ganses en avant ·
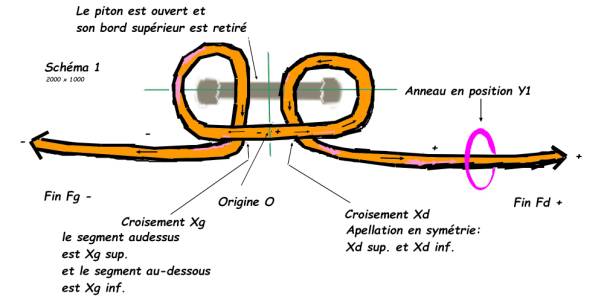
La
manipulation consistera donc à ramener dans les espaces avants du plan du
piton [l’anse et les 2 ganses de A et B] : C’est le système de cordage
en entier qui viendra « de l’arrière cuisine » par
le trou du piton pour faire passer l’anneau de la droite vers la gauche puis
on remettra le système de cordage en place.. ·
Au
Final, c’est comme si on faisait
venir le demi-espace arrière droit vers le demi-espace avant droit, et le
demi-espace arrière gauche vers le demi-espace avant-gauche. Puis là, on
réunit les deux-demi espaces avant, on y effectue le passage de l’anneau de
droite à gauche. Puis cela fait, on procède à la remise en place des quarts
d’espaces en en faisant repasser deux à travers le piton. ·
On n’aura
besoin ni d’introduire ni de défaire aucun nouage, ni d’introduire ni de
recoller aucune coupure : des opérations de translation continue
suffiront, mais le tout en 3D, nous reviendrons sur ce point. 1.
Temps 1 : Les deux demi-espaces arrière vont passer en avant – ou du
moins, pour être plus précis, la moitié seulement de chacun de ces deux demi-espaces,
mais leur moitié utile, celle qui est médiane, proche du piton, et de la même
façon on va diviser chacun des deux demi-espaces avant en deux, dont la
partie médiane seule sera une partie utile. Dès l’abord,
seules 2 opérations apparaissent possibles : a)
passer
l’anneau sous l’anse dans le « demi-espace avant droit » (le quart
de l’espace total) ce qui va diviser le segment A) en deux parties bien
distinctes appartenant l’une à la partie médiane utile de cet espace et
l’autre distale inutile. b)
ramener des
« espaces arrières » vers les « espaces avants » à
travers le trou du piton les 2 ganses Mais si on commençait par b), l’anneau se retrouverait
maintenant engagé vers « le demi-espace arrière droit » par rapport
au « plan du piton » sans pouvoir l'atteindre et le système des 2
ganses restant en avant bloquerait aussi le passage vers la gauche. On n’a
fait que bloquer les positions ! Il faut donc au contraire réaliser d’abord a) : Ainsi le
segment A) se trouve décomposé en 2 parts, puis plus rien n’empêche plus
alors de faire venir le paquet des deux ganses de l’arrière en avant et
l’anneau déjà en avant se trouvera libre de circuler de droite à gauche ou
inversement C’est donc l’ordre des opérations qu’il faut choisir. Dans le
détail : a)
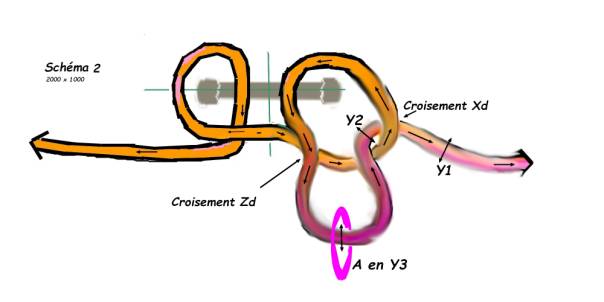
Faire venir
l’anneau au-dessus de l’anse centrale après avoir tirée l’anse suffisamment
pour le faire (en passant l'anneau d’abord sous elle, puis derrière vers le
haut, puis au-dessus vers l’avant) (ce qui va former une boucle) b)
Afin de
pouvoir faire sortir par le trou du piton (de l’arrière vers l'avant)
l’ensemble composé des 2 ganses symétriques (4 brins) + la partie médiane de
l’anse maintenant porteuse de l’anneau, également par le trou du piton
d’arrière en avant. 2.
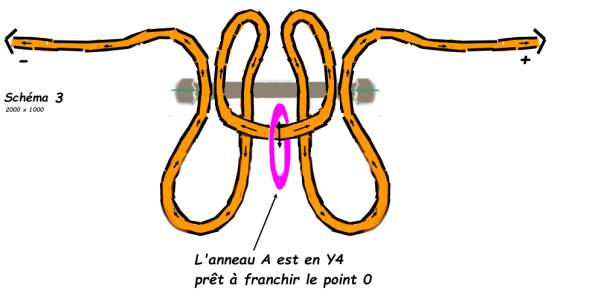
Temps
médian : Le tour est joué car dès lors tout le
dispositif, devenu très lâche, est dans l’espace antérieur et l’anneau pourra
changer librement de côté en passant librement dans la ganse de droite puis
dans la ganse de gauche qui lui forment un tunnel – ce qu'on ne pouvait pas
faire à cause du piton) 3.
Mise en
place inverse :
Il faut ensuite refaire
les deux opérations a) et b) de façon inverse et symétrique en repassant par
le trou du piton les deux ganses et la partie médiane de l’anse et sortir
enfin l’anneau de la boucle de l’anse qui est maintenant à gauche et divise
en 2 le segment B), cette fois par-dessus vers l’arrière puis vers le bas
puis vers l’avant par-dessous. Représentation
schématique :
REMARQUE
2 : « Les 1001 nuits
scientifiques » dans Spirou Cette
figure de topologie a figuré,
présentée différemment, intégrée dans une série de bandes dessinées appelée
« Les mille et unes nuits scientifiques épisode N°6 page
21 clic »
dans le journal Spirou - et dont l’auteur Jean Pierre Petit est devenu
astrophysicien renommé. J.P. Petit
présente maintenant en ligne gratuitement la quasi-intégralité de ses
productions, B.D et textes, et présente actuellement son dernier travail
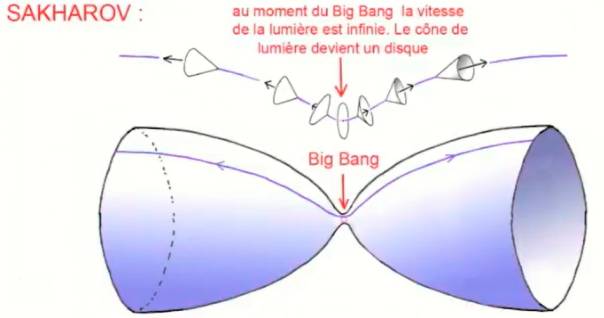
« l’Univers Janus » Les travaux
de J.P Petit ont toujours été orientés par la prise en compte des symétries
(du Retournement de la Sphère à L'univers à masse négative) Il est
possible que cette figure topologique soit annonciatrice de la modélisation
de son « Univers Janus » avec ses deux parties, le passé et le futur
et l’inversion des flèches du temps. A l’image de
l’anneau dans cette figure de topologie, pour entrer dans un monde
énantiomorphe (en miroir) il faudrait soit avoir des amarres je ne sais de
quelles dimensions, soit larguer tout !
|
||||||||||||||||||||||||